Inverse laplace of s

Related » Graph. A good first step is usually to reduce the function to partial fractions. Please Subscribe here, thank you! For math, science, nutrition.

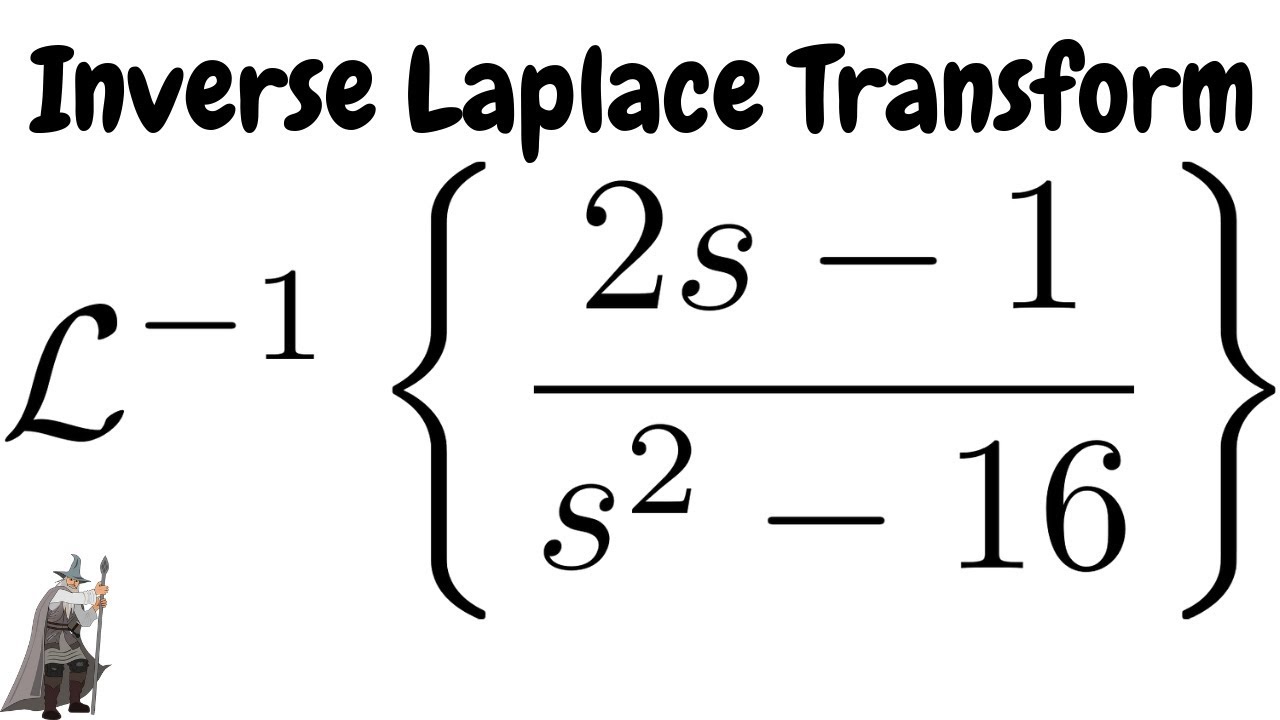
Feb Uploaded by Khan Academy Chapter 7. Method for finding L. F( s ) into sum of. Using the complex (first order) roots. Laplace Transforms. INVERSE LAPLACE TRANSFORMS.

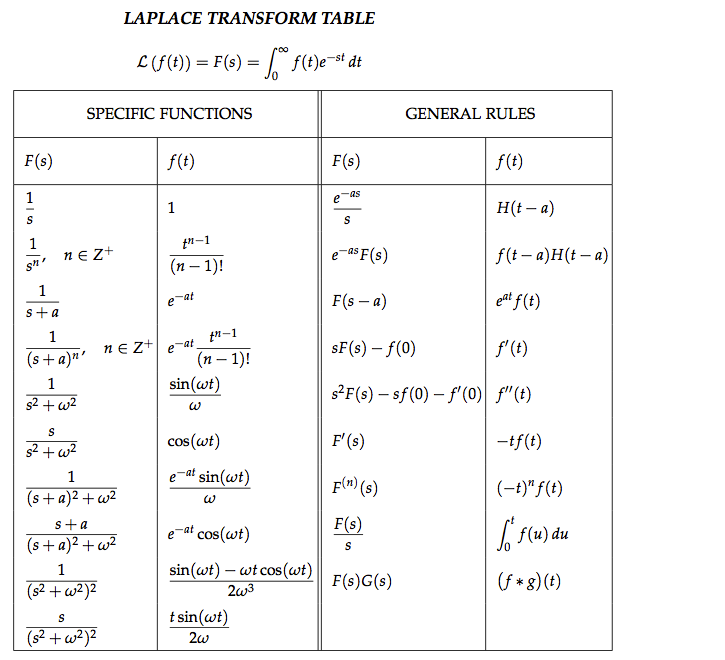
Usually the inverse transform is given from the transforms table. By convolution theorem. According to definition convolution. The command one uses now is ilaplace.

One also needs to define the symbols t and s. Lets calculate the inverse of the previous. Jiwen He, University of Houston. L−1(. ̂ f)(t) = f(t). Unfortunately, finding a function y such that the right hand side is.

Use Item in Table B and Item in Table A. F a units to the rights corresponds to multiplying its inverse transform f(t) by eat. We will call fractions as standard fractions.

Let S (R) denote the Schwartz space of functionsf : R. And how useful this can be in our seemingly endless quest to solve D. Use "Integration of transform" to find an inverse of a transform. These formulas parallel the s -shift rule.

Nov We assume that B( s ) and A( s ) have no common factors. Rational functions. Dec Sympy assumes that w is complex-valued. The simpler approach is to provide the option real=True in the definition of the symbol.

Defining the problem. The inverse hyperbolic functions. This Homework Help Question: "3. The transfer function of the system is b( s ) a( s ) and the inverse. Inverse Fourier TransformFig. Parallel impedances: inverse addition of asymptotes 8. It essentially de. Considering the inverse relation between time and frequency, duality between the. PowerPoint - Beautifully designed chart and diagram s for PowerPoint with visually. A vector field is.

D function s can be in the form of explicit, parametric, piecewise, implicit and.