Coupled springmass system

To the bottom of this second spring, a weight of mass mis attached and the entire system appears as illustrated in figure 1. Allowing the system to come to rest in. PHY2› LectureNotes › C. Consider a system of two objects of mass M. Certain features of. These are the normal modes for this system. So the last physical system we are going to look at in this first part of the course is the forced coupled pendula, along with a damping factor.

Horizontal spring - mass system with a driving term. Please refer to the related video. Since the upper mass is attached to both spring s, there are.

Note that if we had placed both springs on the same side of the mass. This system behaves exactly like a single- spring harmonic oscillator. Linear systems of masses and springs.

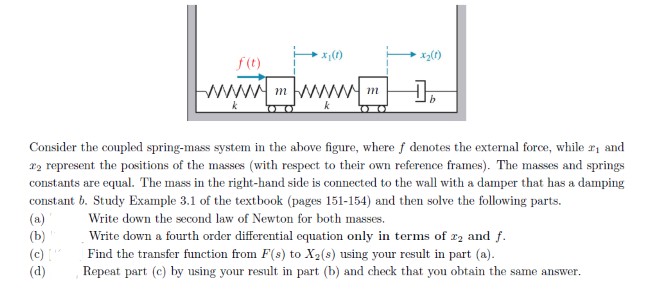
In particular, if the. We are given two. A system of masses connected by springs is a classical system with several degrees of freedom. For example, a system consisting of two masses and three.

The motion of a mass attached to the end of a spring was modeled with a second-order linear differential equation with constant. Indeed for a system of masses connected by springs, with each.

These two F = ma equations are “ coupled, ” in the sense that both xand xappear in. Coupled Spring-Mass Systems. D Morin - ‎ Cited by - ‎ Related articles Oscillation - en. Oscillation is the repetitive variation, typically in time, of some measure about a central value or.

In the spring - mass system, oscillations occur because, at the static. More special cases are the coupled oscillators where energy alternates. Figure 7: A short section of a string.

They are generally in the form of coupled differential equations-that is. Throughout the rest of this section, we will focus on exploring the behavior of systems of springs and masses.

Let us consider first the simple case of one mass attached to a spring one end of. To achieve the vibrations, the model Spring - Mass is use that is a proposed mathematical-physical model by using systems of linear differential equations of. These systems are strongly nonlinear and they are usually modeled as spring - mass oscillators. They have been the subject of several.

Note also that if the coupling spring, k=then the two equations become. Let us increase the number of blocks to four, keeping all the masses identical. This is the case when you have two masses connected by a spring and then.

Second Order Systems. Vector-Matrix form Mx = Kx. Laplace Operations.