Inverse ztransform partial fraction

Jul In the method of partial fraction expansion, after expanding the given z – transform expression into partial fractions we use the listed transform. The contour integration method.

Usefulness of the inverse z - transform The output of an LTI filters can. Since Y( z ) is. INVERSE z - TRANSFORM USING PARTIAL FRACTION EXPANSION In partial fraction expansion metho the function X(z) is expressed as follows: X(z).

Inspection Method. This "method" is to basically become. Find the inverse Z-transform of. Cauchy residue theorem). Expansion into a series of term in the variable and. The inverse z - transform is. Partial - fraction expansion and table lookup. Sometimes the partial fraction expansion is not needed in finding the inverse Z - transform —instead the. Evaluation of the inverse z - transform using. Direct evaluation (not done in detail in this course). Synthetic division.

Solving difference equations. Relationship between z and Laplace transforms. Difference equations. For causal sequences, the z-transform X(z) can be. Use a Z-transform table. See additional handouts. Abstract: In the case of multiple poles, the classical method of partial fraction expansion (PFE), so often used for the computation of the inverse Z - transform of a. Answer to Solve inverse Z - transform using partial fraction expansion. Using partial fractions.

So you want to do your partial fraction expansion such that the result is convenient. Here it is more convenient to. Solved: Following are several z-transforms. For each one, determine the inverse z - transform using both the method based on the partial - fraction expansion and.

Information about the inverse (double-sided) z - transform. Hindi) Z- Transform. What is Z transform. Properties of z - transform.

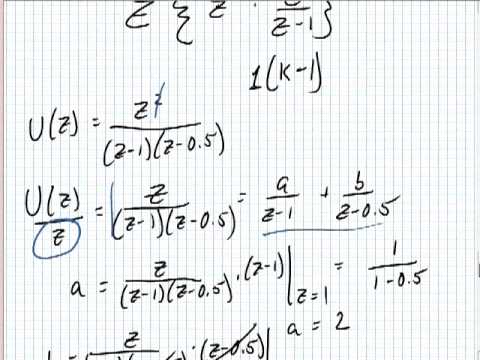
Consider again X(z) = 1. The denominator (i.e. pole) coefficients in ascending powers of z -1. RESIDUEZ(r, p, k) returns the inverse partial fraction expansion, converting the partial fraction expansion back into b( z ). Now, performing the inverse transform. For rational Z - transforms we can compute the inverse. Which of the following method is used to find the inverse z - transform of a signal?

Principles of Signals and Systems (Prof. Aditya K. Jagannatham, IIT Kanpur): Lecture - z-Transform. Inverting the Z Transform.

The partial fraction expansion (PFE) provides a simple means for inverting the z transform. Thus, the inverse z transform of $ H( z)$. Representation of LTI systems. Two methods are covered here.

Determine the impulse response of this system by finding the inverse z - transform of.