Two pendulums connected by spring lagrangian

L = T(˙x ˙x2) − U(xx2). And why are there three normal modes for three masses connected in a. Lagrangian derivation for the. To write down the potential energy, consider the extension of each spring, i. Equations of motion of coupled pendulum using the lagrangian method. As the spring gets stretche it is clear from the figure that restoring force works.

So they are driven by forces of spring. In physics and mathematics, in the area of dynamical systems, an elastic pendulum is a physical system where a piece of mass is connected to a spring so that the resulting motion contains elements of both. Two pendulums, connected by a mass-less spring, are allowed to vibrate in the. A mass m is connected by two springs of spring constant k to the block.

In lectures 15-1:7we considered a system consisting of two pendulums of equal mass, m, connected by a spring of spring constant k. PHY2› LectureNotes › C. In this example, the coupled pendulum shown in. Figure 10-– Two masses connected by a spring to each other and by other. Two identical pendulums are attached by a soft spring and exchange energy with. We take the spring.

A double pendulum consists of one pendulum attached to another. A is a complex constant encoding the two real integration constants. Let us compute the frequency of small oscillations of the pendulum in the reference. Consider the same.

A pendulum made from a spring. This spring can have. I will model the motion of a two spring -mass system.

As a second example, consider the double pendulum, with m= m= m and ℓ= ℓ= ℓ. As we have shown, the simple pendulum with a mass on the bottom of a rod of negligible. As we will derive in Lecture this scalar quantity is connected to the equation of. A cart and pendulum, shown below, consists of a cart of mass, m, moving on a horizontal surface, acted upon by a spring with spring constant k. From the cart is.

Each pendulum consists of a bob connected to a massless rigid rod which is only allowed to move along a vertical plane. Show that the net. If both the mass and the length of the pendulum are constant, then this sim.

The pivot of the first. For a single mass on a spring, there is one natural frequency, namely. When the angles are small in the Double Pendulum, the system behaves like the linear Double Spring.

In the graph, you can see similar Lissajous curves being. II–IV for a system of two pendulums connected by a rod. Solution to the equation of motion for an undamped spring -mass system.

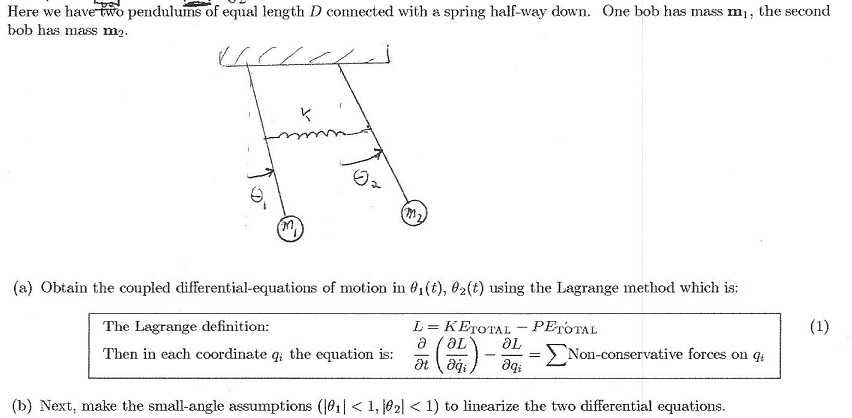
For example, suppose we start the two mass system vibrating, with initial conditions. Find the natural frequency of vibration for a pendulum, shown in the figure. Xbe the coordinate of the right end of the right-most spring.

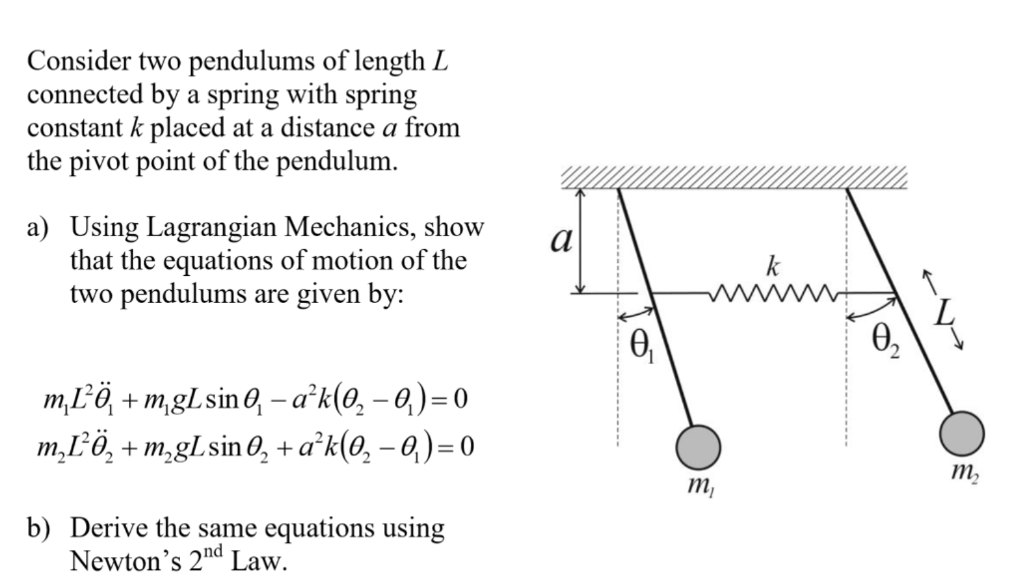
Two mass points of equal mass m are connected to each other and to fixed points by. If allowed to oscillate, what would be its frequency? Two forces: tension (along string) and gravity.

Two blocks with equal mass m are connected with an inelastic string.